What Is the Equation of the Line Tangent to the Curve Xy + 1 + E = Eã¢ë†â€™xy at the Point (1, âë†â€™1)?
Vectors in Infinite
9 Vectors in Three Dimensions
Learning Objectives
- Depict three-dimensional space mathematically.
- Locate points in space using coordinates.
- Write the distance formula in three dimensions.
- Write the equations for uncomplicated planes and spheres.
- Perform vector operations in
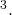
Vectors are useful tools for solving two-dimensional issues. Life, however, happens in three dimensions. To expand the use of vectors to more realistic applications, information technology is necessary to create a framework for describing three-dimensional space. For example, although a two-dimensional map is a useful tool for navigating from i identify to some other, in some cases the topography of the land is important. Does your planned route become through the mountains? Practice you take to cross a river? To appreciate fully the impact of these geographic features, you must use three dimensions. This section presents a natural extension of the two-dimensional Cartesian coordinate airplane into three dimensions.
Three-Dimensional Coordinate Systems
Every bit nosotros accept learned, the ii-dimensional rectangular coordinate system contains two perpendicular axes: the horizontal 10-axis and the vertical y-axis. We tin can add a third dimension, the z-axis, which is perpendicular to both the ten-axis and the y-axis. We phone call this system the iii-dimensional rectangular coordinate organisation. It represents the three dimensions we meet in real life.
Definition
The iii-dimensional rectangular coordinate system consists of three perpendicular axes: the x-axis, the y-axis, and the z-axis. Considering each centrality is a number line representing all real numbers in ![]() the three-dimensional system is often denoted by
the three-dimensional system is often denoted by ![]()
In (Figure)(a), the positive z-axis is shown to a higher place the aeroplane containing the x– and y-axes. The positive x-axis appears to the left and the positive y-axis is to the right. A natural question to ask is: How was arrangement determined? The system displayed follows the right-paw dominion. If we have our right hand and align the fingers with the positive x-centrality, so ringlet the fingers and then they point in the direction of the positive y-axis, our thumb points in the direction of the positive z-axis. In this text, we always piece of work with coordinate systems set upward in accordance with the correct-paw dominion. Some systems do follow a left-hand rule, simply the right-hand rule is considered the standard representation.
(a) Nosotros can extend the ii-dimensional rectangular coordinate system by adding a 3rd axis, the z-axis, that is perpendicular to both the x-axis and the y-axis. (b) The right-manus rule is used to decide the placement of the coordinate axes in the standard Cartesian aeroplane.
In ii dimensions, nosotros describe a bespeak in the plane with the coordinates ![]() Each coordinate describes how the signal aligns with the corresponding axis. In three dimensions, a new coordinate,
Each coordinate describes how the signal aligns with the corresponding axis. In three dimensions, a new coordinate, ![]() is appended to betoken alignment with the z-centrality:
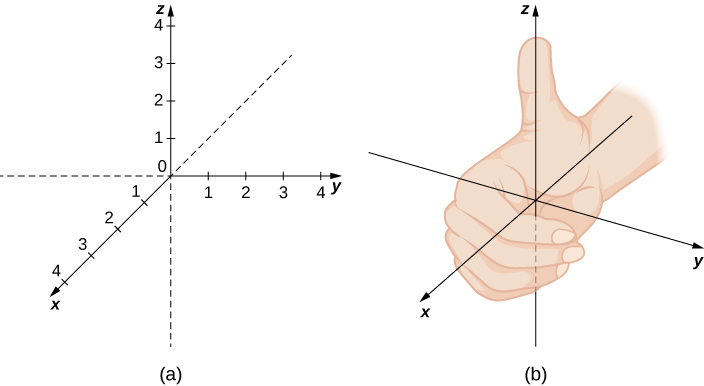
is appended to betoken alignment with the z-centrality: ![]() A point in space is identified by all three coordinates ((Figure)). To plot the point
A point in space is identified by all three coordinates ((Figure)). To plot the point ![]() go x units along the x-axis, and then
go x units along the x-axis, and then ![]() units in the direction of the y-axis, then
units in the direction of the y-axis, then ![]() units in the direction of the z-axis.
units in the direction of the z-axis.
Locating Points in Space
Sketch the point ![]() in iii-dimensional space.
in iii-dimensional space.
Sketch the signal ![]() in 3-dimensional infinite.
in 3-dimensional infinite.
Hint
Start by sketching the coordinate axes. Then sketch a rectangular prism to help find the point in space.
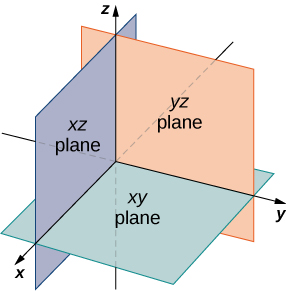
In 2-dimensional space, the coordinate plane is defined by a pair of perpendicular axes. These axes allow us to name any location within the plane. In three dimensions, we define coordinate planes by the coordinate axes, only as in 2 dimensions. There are three axes now, so at that place are three intersecting pairs of axes. Each pair of axes forms a coordinate plane: the xy-aeroplane, the xz-airplane, and the yz-plane ((Figure)). Nosotros ascertain the xy-plane formally equally the following prepare: ![]() Similarly, the xz-plane and the yz-airplane are divers as
Similarly, the xz-plane and the yz-airplane are divers as ![]() and
and ![]() respectively.
respectively.
To visualize this, imagine you lot're building a house and are standing in a room with merely two of the iv walls finished. (Assume the ii finished walls are adjacent to each other.) If you lot stand with your dorsum to the corner where the two finished walls meet, facing out into the room, the floor is the xy-plane, the wall to your right is the xz-plane, and the wall to your left is the yz-airplane.
The plane containing the ten– and y-axes is called the xy-airplane. The plane containing the x– and z-axes is chosen the xz-plane, and the y– and z-axes define the yz-aeroplane.
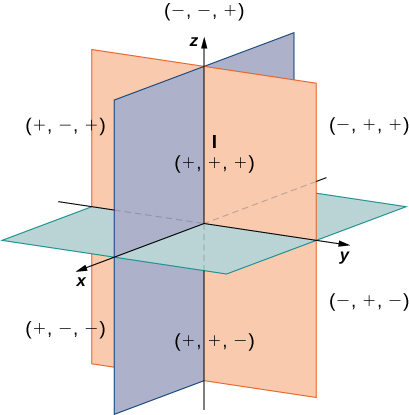
In two dimensions, the coordinate axes partition the plane into 4 quadrants. Similarly, the coordinate planes divide space between them into eight regions well-nigh the origin, called octants. The octants fill ![]() in the same fashion that quadrants fill
in the same fashion that quadrants fill ![]() as shown in (Effigy).
as shown in (Effigy).
Points that lie in octants take iii nonzero coordinates.
Most work in iii-dimensional space is a comfy extension of the respective concepts in ii dimensions. In this section, nosotros use our cognition of circles to draw spheres, and so we expand our understanding of vectors to three dimensions. To achieve these goals, nosotros begin past adapting the distance formula to three-dimensional space.
If two points prevarication in the same coordinate plane, then it is straightforward to calculate the distance between them. We that the altitude ![]() between two points
between two points ![]() and
and ![]() in the xy-coordinate plane is given past the formula
in the xy-coordinate plane is given past the formula
![]()
The formula for the altitude betwixt ii points in space is a natural extension of this formula.
The Distance between Two Points in Space
The altitude ![]() between points
between points ![]() and
and ![]() is given by the formula
is given by the formula
![]()
The proof of this theorem is left as an exercise. (Hint: First notice the distance ![]() betwixt the points
betwixt the points ![]() and
and ![]() as shown in (Figure).)
as shown in (Figure).)
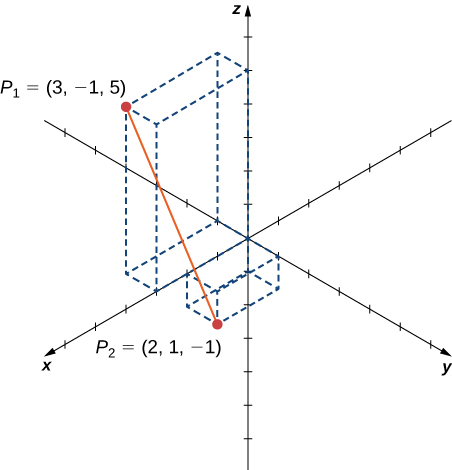
Altitude in Infinite
Notice the distance betwixt points ![]() and
and ![]()
Detect the distance between the two points.
Substitute values directly into the altitude formula:
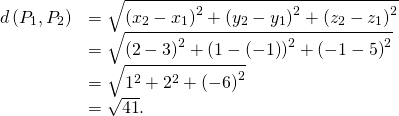
Observe the distance between points ![]() and
and ![]()
![]()
Hint
![]()
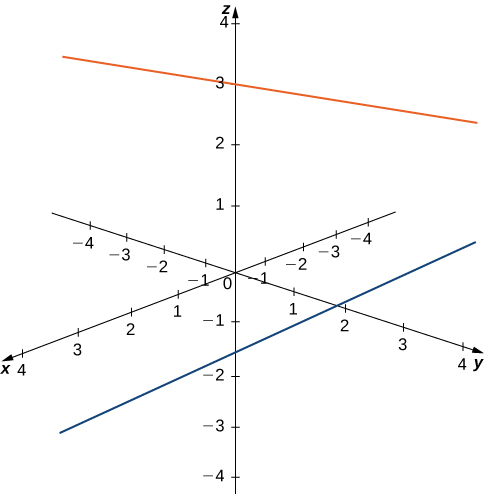
Earlier moving on to the next section, allow's get a experience for how ![]() differs from
differs from ![]() For instance, in
For instance, in ![]() lines that are non parallel must always intersect. This is not the instance in
lines that are non parallel must always intersect. This is not the instance in ![]() For case, consider the line shown in (Effigy). These ii lines are non parallel, nor practise they intersect.
For case, consider the line shown in (Effigy). These ii lines are non parallel, nor practise they intersect.
These two lines are non parallel, but still practise not intersect.
You lot tin can also take circles that are interconnected but accept no points in common, as in (Figure).
These circles are interconnected, simply take no points in common.
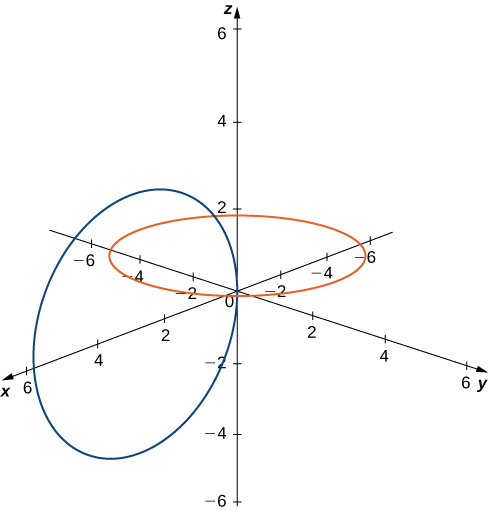
Nosotros have a lot more flexibility working in three dimensions than nosotros practice if nosotros stuck with simply two dimensions.
Writing Equations in ℝthree
At present that we tin can represent points in space and notice the distance between them, we tin can learn how to write equations of geometric objects such as lines, planes, and curved surfaces in ![]() First, we start with a simple equation. Compare the graphs of the equation
First, we start with a simple equation. Compare the graphs of the equation ![]() in
in ![]() ((Figure)). From these graphs, we can come across the same equation tin can describe a bespeak, a line, or a plane.
((Figure)). From these graphs, we can come across the same equation tin can describe a bespeak, a line, or a plane.
In space, the equation ![]() describes all points
describes all points ![]() This equation defines the yz-airplane. Similarly, the xy-plane contains all points of the form
This equation defines the yz-airplane. Similarly, the xy-plane contains all points of the form ![]() The equation
The equation ![]() defines the xy-plane and the equation
defines the xy-plane and the equation ![]() describes the xz-plane ((Figure)).
describes the xz-plane ((Figure)).
(a) In space, the equation ![]() describes the xy-airplane. (b) All points in the xz-plane satisfy the equation
describes the xy-airplane. (b) All points in the xz-plane satisfy the equation ![]()
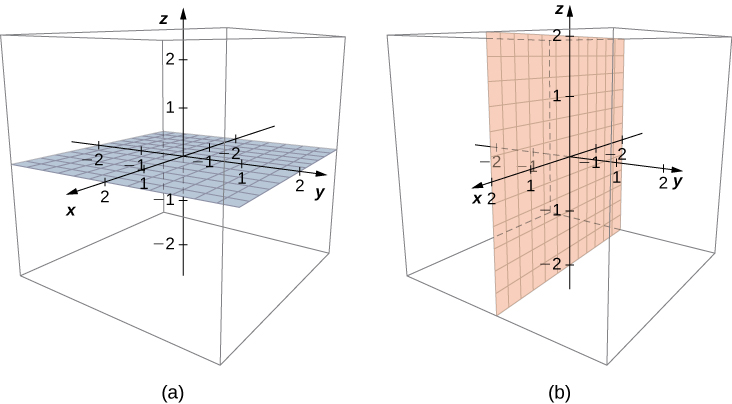
Understanding the equations of the coordinate planes allows us to write an equation for any airplane that is parallel to one of the coordinate planes. When a plane is parallel to the xy-airplane, for case, the z-coordinate of each signal in the plane has the aforementioned constant value. But the 10– and y-coordinates of points in that plane vary from point to point.
Write an equation of the aeroplane passing through betoken ![]() that is parallel to the xy-plane.
that is parallel to the xy-plane.
![]()
Hint
If a plane is parallel to the xy-plane, the z-coordinates of the points in that aeroplane do not vary.
As we have seen, in ![]() the equation
the equation ![]() describes the vertical line passing through point
describes the vertical line passing through point ![]() This line is parallel to the y-axis. In a natural extension, the equation
This line is parallel to the y-axis. In a natural extension, the equation ![]() in
in ![]() describes the plane passing through indicate
describes the plane passing through indicate ![]() which is parallel to the yz-plane. Another natural extension of a familiar equation is constitute in the equation of a sphere.
which is parallel to the yz-plane. Another natural extension of a familiar equation is constitute in the equation of a sphere.
Definition
A sphere is the set of all points in space equidistant from a fixed indicate, the center of the sphere ((Effigy)), just as the set of all points in a plane that are equidistant from the center represents a circumvolve. In a sphere, equally in a circle, the distance from the center to a point on the sphere is called the radius.
Each point ![]() on the surface of a sphere is
on the surface of a sphere is ![]() units away from the center
units away from the center ![]()
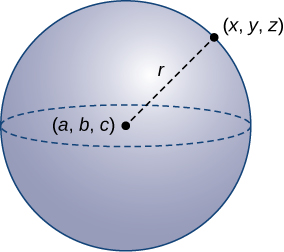
The equation of a circle is derived using the altitude formula in 2 dimensions. In the same way, the equation of a sphere is based on the three-dimensional formula for altitude.
Rule: Equation of a Sphere
The sphere with eye ![]() and radius
and radius ![]() can be represented by the equation
can be represented by the equation
![]()
This equation is known every bit the standard equation of a sphere.
Finding an Equation of a Sphere
Find the standard equation of the sphere with center ![]() and point
and point ![]() every bit shown in (Figure).
every bit shown in (Figure).
The sphere centered at ![]() containing bespeak
containing bespeak ![]()
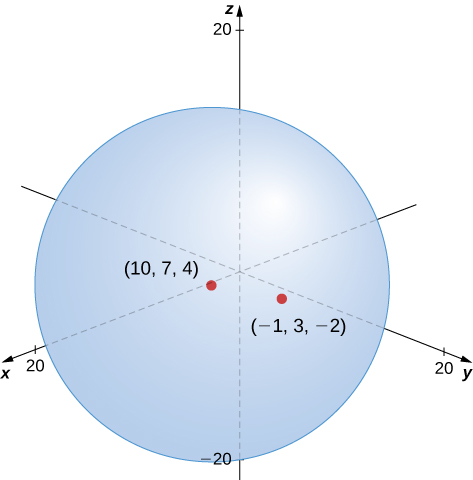
Utilise the distance formula to find the radius ![]() of the sphere:
of the sphere:
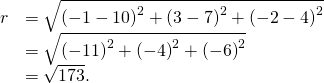
The standard equation of the sphere is
![]()
Find the standard equation of the sphere with heart ![]() containing indicate
containing indicate ![]()
![]()
Hint
First apply the altitude formula to find the radius of the sphere.
Finding the Equation of a Sphere
Let ![]() and
and ![]() and suppose line segment
and suppose line segment ![]() forms the diameter of a sphere ((Figure)). Find the equation of the sphere.
forms the diameter of a sphere ((Figure)). Find the equation of the sphere.
Line segment ![]()
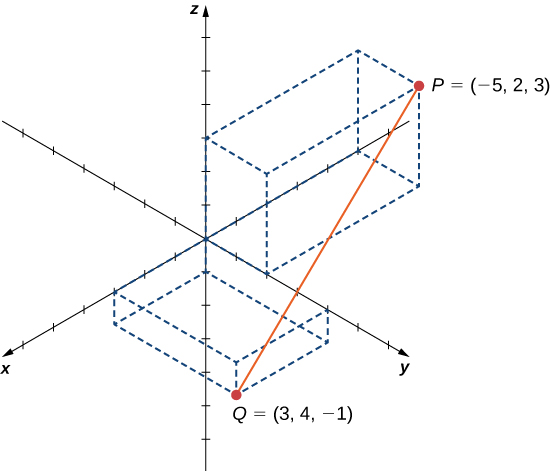
Since ![]() is a bore of the sphere, nosotros know the heart of the sphere is the midpoint of
is a bore of the sphere, nosotros know the heart of the sphere is the midpoint of ![]() And then,
And then,
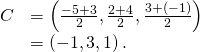
Furthermore, nosotros know the radius of the sphere is half the length of the diameter. This gives
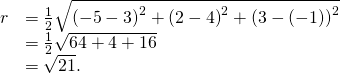
And so, the equation of the sphere is ![]()
Find the equation of the sphere with diameter ![]() where
where ![]() and
and ![]()
![]()
Hint
Find the midpoint of the diameter first.
Graphing Other Equations in 3 Dimensions
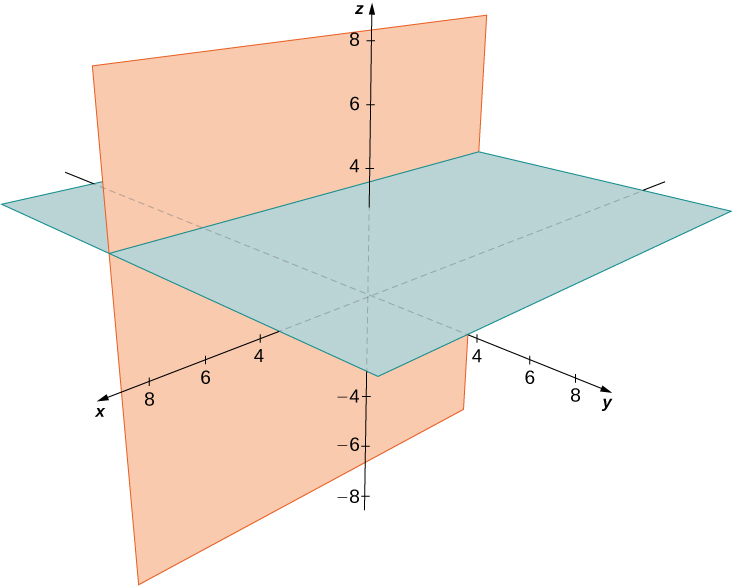
Describe the set of points that satisfies ![]() and graph the set.
and graph the set.
Draw the set of points that satisfies ![]() and graph the set.
and graph the set.
The prepare of points forms the ii planes ![]() and
and ![]()
Hint
One of the factors must be zero.
Graphing Other Equations in Three Dimensions
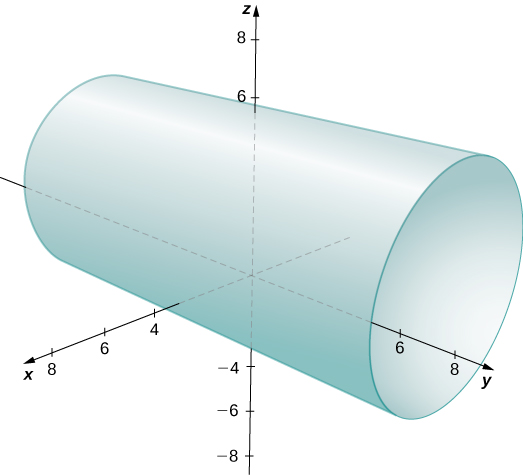
Describe the gear up of points in three-dimensional space that satisfies ![]() and graph the set.
and graph the set.
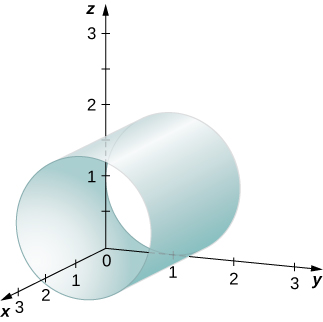
Draw the gear up of points in three dimensional space that satisfies ![]() and graph the surface.
and graph the surface.
A cylinder of radius 4 centered on the line with ![]()
Hint
Think about what happens if yous plot this equation in ii dimensions in the xz-plane.
Working with Vectors in ℝ3
Merely like two-dimensional vectors, three-dimensional vectors are quantities with both magnitude and management, and they are represented by directed line segments (arrows). With a 3-dimensional vector, nosotros utilize a three-dimensional arrow.
3-dimensional vectors can also exist represented in component grade. The notation ![]() is a natural extension of the ii-dimensional instance, representing a vector with the initial point at the origin,
is a natural extension of the ii-dimensional instance, representing a vector with the initial point at the origin, ![]() and last point
and last point ![]() The zero vector is
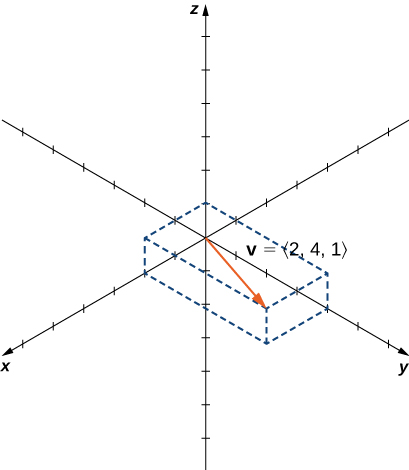
The zero vector is ![]() And so, for example, the three dimensional vector
And so, for example, the three dimensional vector ![]() is represented by a directed line segment from betoken
is represented by a directed line segment from betoken ![]() to point
to point ![]() ((Figure)).
((Figure)).
Vector ![]() is represented by a directed line segment from point
is represented by a directed line segment from point ![]() to point
to point ![]()
."">  ."">
."">
Vector addition and scalar multiplication are defined analogously to the two-dimensional case. If ![]() and
and ![]() are vectors, and
are vectors, and ![]() is a scalar, then
is a scalar, then
![]()
If ![]() then
then ![]() is written as
is written as ![]() and vector subtraction is defined by
and vector subtraction is defined by ![]()
The standard unit of measurement vectors extend hands into three dimensions as well—![]()
![]() and
and ![]() —and we use them in the aforementioned mode we used the standard unit vectors in two dimensions. Thus, we tin represent a vector in
—and we use them in the aforementioned mode we used the standard unit vectors in two dimensions. Thus, we tin represent a vector in ![]() in the following ways:
in the following ways:
![]()
Vector Representations
Let ![]() exist the vector with initial point
exist the vector with initial point ![]() and terminal point
and terminal point ![]() every bit shown in (Effigy). Express
every bit shown in (Effigy). Express ![]() in both component grade and using standard unit vectors.
in both component grade and using standard unit vectors.
The vector with initial point ![]() and terminal point
and terminal point ![]()
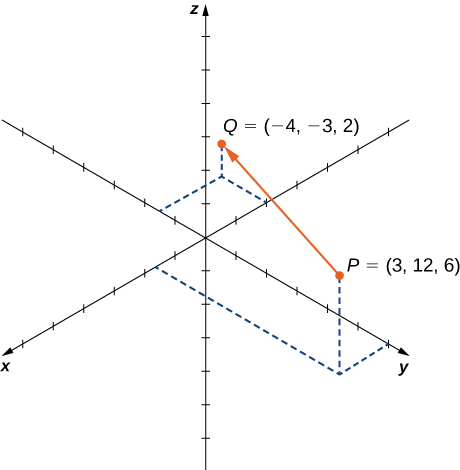
In component form,
![]()
In standard unit grade,
![]()
Permit ![]() and
and ![]() Express
Express ![]() in component form and in standard unit form.
in component form and in standard unit form.
![]()
Hint
Write ![]() in component class first.
in component class first. ![]() is the terminal point of
is the terminal point of ![]()
Equally described earlier, vectors in 3 dimensions bear in the same way every bit vectors in a plane. The geometric estimation of vector addition, for example, is the aforementioned in both two- and three-dimensional space ((Figure)).
To add vectors in three dimensions, nosotros follow the same procedures nosotros learned for 2 dimensions.
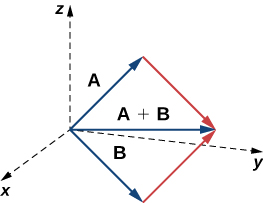
We have already seen how some of the algebraic properties of vectors, such as vector add-on and scalar multiplication, tin be extended to 3 dimensions. Other properties tin be extended in similar fashion. They are summarized here for our reference.
Rule: Properties of Vectors in Space
Permit ![]() and
and ![]() be vectors, and let
be vectors, and let ![]() be a scalar.
be a scalar.
Scalar multiplication: ![]()
Vector add-on: ![]()
Vector subtraction: ![]()
Vector magnitude: ![]()
Unit vector in the management of five: ![]() if
if ![]()
We have seen that vector add-on in 2 dimensions satisfies the commutative, associative, and additive inverse properties. These backdrop of vector operations are valid for 3-dimensional vectors as well. Scalar multiplication of vectors satisfies the distributive property, and the nada vector acts as an condiment identity. The proofs to verify these properties in three dimensions are straightforward extensions of the proofs in ii dimensions.
- Get-go, apply scalar multiplication of each vector, so decrease:
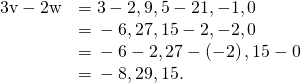
- Write the equation for the magnitude of the vector, and so use scalar multiplication:
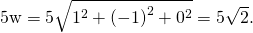
- First, utilise scalar multiplication, then find the magnitude of the new vector. Note that the result is the aforementioned as for part b.:
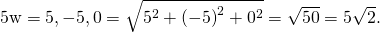
- Recall that to detect a unit of measurement vector in two dimensions, we carve up a vector past its magnitude. The process is the same in 3 dimensions:
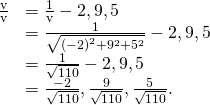
Let ![]() and
and ![]() Find a unit vector in the management of
Find a unit vector in the management of ![]()
![]()
Hint
Start by writing ![]() in component class.
in component class.
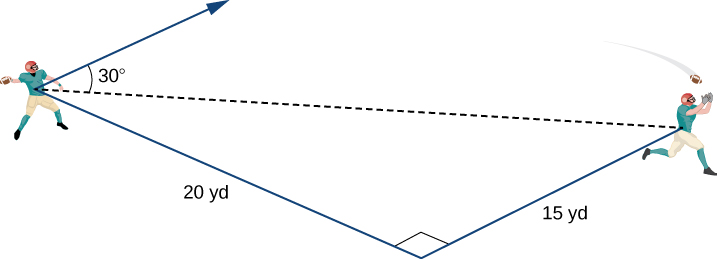
Throwing a Forwards Pass
A quarterback is continuing on the football field preparing to throw a pass. His receiver is standing 20 yd down the field and 15 yd to the quarterback'south left. The quarterback throws the ball at a velocity of 60 mph toward the receiver at an upward bending of ![]() (see the following figure). Write the initial velocity vector of the ball,
(see the following figure). Write the initial velocity vector of the ball, ![]() in component grade.
in component grade.
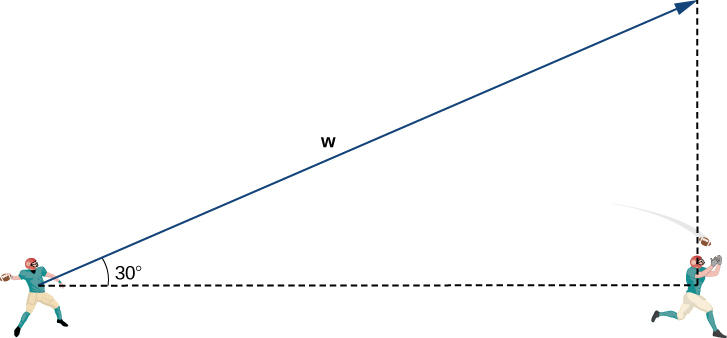
The first affair we desire to do is find a vector in the aforementioned management equally the velocity vector of the ball. We then calibration the vector appropriately so that information technology has the right magnitude. Consider the vector ![]() extending from the quarterback'south arm to a betoken directly in a higher place the receiver'southward head at an angle of
extending from the quarterback'south arm to a betoken directly in a higher place the receiver'southward head at an angle of ![]() (meet the following figure). This vector would take the aforementioned direction as
(meet the following figure). This vector would take the aforementioned direction as ![]() but it may not have the right magnitude.
but it may not have the right magnitude.
The receiver is 20 yd down the field and 15 yd to the quarterback'southward left. Therefore, the direct-line distance from the quarterback to the receiver is
![]()
We have ![]() So the magnitude of
So the magnitude of ![]() is given by
is given by
![]()
and the vertical distance from the receiver to the terminal point of ![]() is
is
![]()
So ![]() and has the same direction as
and has the same direction as ![]()
Recall, though, that we calculated the magnitude of ![]() to be
to be ![]() and
and ![]() has magnitude
has magnitude ![]() mph. Then, we need to multiply vector
mph. Then, we need to multiply vector ![]() by an advisable constant,
by an advisable constant, ![]() We want to find a value of
We want to find a value of ![]() so that
so that ![]() mph. Nosotros have
mph. Nosotros have
![]()
and so we want
*** QuickLaTeX cannot compile formula: \begin{assortment}{}\\ \\ \hfill k\frac{50}{\sqrt{iii}}& =\hfill & 60\hfill \\ \hfill g& =\hfill & \frac{threescore\sqrt{iii}}{50}\hfill \\ \hfill k& =\hfill & \frac{6\sqrt{iii}}{5}.\hfill \finish{assortment} *** Fault message: Missing # inserted in alignment preamble. leading text: $\begin{array}{} Missing $ inserted. leading text: ...n{assortment}{}\\ \\ \hfill thousand\frac{fifty}{\sqrt{three}} Extra }, or forgotten $. leading text: ...n{array}{}\\ \\ \hfill k\frac{fifty}{\sqrt{3}} Missing } inserted. leading text: ...{array}{}\\ \\ \hfill m\frac{50}{\sqrt{3}}& Extra }, or forgotten $. leading text: ...{array}{}\\ \\ \hfill yard\frac{50}{\sqrt{3}}& Missing } inserted. leading text: ...{array}{}\\ \\ \hfill k\frac{50}{\sqrt{3}}& Actress }, or forgotten $. leading text: ...{assortment}{}\\ \\ \hfill k\frac{50}{\sqrt{3}}& Missing } inserted. leading text: ...{array}{}\\ \\ \hfill k\frac{fifty}{\sqrt{3}}& Extra }, or forgotten $. leading text: ...{array}{}\\ \\ \hfill yard\frac{50}{\sqrt{3}}& Missing } inserted. And so
![]()
Permit's double-cheque that ![]() We have
We have
![]()
So, nosotros have institute the correct components for ![]()
Assume the quarterback and the receiver are in the same identify equally in the previous example. This time, all the same, the quarterback throws the ball at velocity of ![]() mph and an angle of
mph and an angle of ![]() Write the initial velocity vector of the ball,
Write the initial velocity vector of the ball, ![]() in component class.
in component class.
![]()
Hint
Follow the process used in the previous instance.
Primal Concepts
Fundamental Equations
Consider a rectangular box with 1 of the vertices at the origin, as shown in the following figure. If betoken ![]() is the opposite vertex to the origin, then find
is the opposite vertex to the origin, then find
- the coordinates of the other six vertices of the box and
- the length of the diagonal of the box determined by the vertices
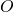 and
and 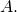
a. ![]() b.
b. ![]()
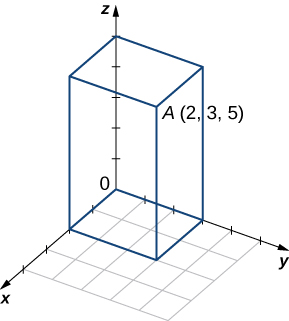
Find the coordinates of signal ![]() and determine its distance to the origin.
and determine its distance to the origin.
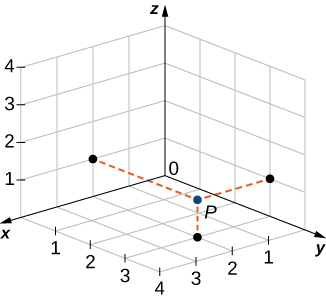
For the post-obit exercises, describe and graph the prepare of points that satisfies the given equation.
![]()
A union of two planes: ![]() (a plane parallel to the xz-plane) and
(a plane parallel to the xz-plane) and ![]() (a plane parallel to the xy-airplane)
(a plane parallel to the xy-airplane)
![]()
![]()
A cylinder of radius ![]() centered on the line
centered on the line ![]()
![]()
Write the equation of the plane passing through bespeak ![]() that is parallel to the xy-plane.
that is parallel to the xy-plane.
![]()
Write the equation of the aeroplane passing through point ![]() that is parallel to the xz-airplane.
that is parallel to the xz-airplane.
Discover an equation of the airplane passing through points ![]()
![]() and
and ![]()
![]()
For the following exercises, find the equation of the sphere in standard form that satisfies the given weather condition.
Center ![]() and radius
and radius ![]()
For the following exercises, discover the center and radius of the sphere with an equation in full general form that is given.
![]()
For the following exercises, express vector ![]() with the initial point at
with the initial point at ![]() and the final signal at
and the final signal at ![]()
- in component form and
- by using standard unit vectors.
![]() and
and ![]()
Discover terminal point ![]() of vector
of vector ![]() with the initial signal at
with the initial signal at ![]()
![]()
For the post-obit exercises, use the given vectors ![]() and
and ![]() to find and express the vectors
to find and express the vectors ![]()
![]() and
and ![]() in component form.
in component form.
![]()
![]()
![]()
![]()
For the post-obit exercises, vectors u and v are given. Find the magnitudes of vectors ![]() and
and ![]()
![]()
![]()
For the following exercises, find the unit vector in the management of the given vector ![]() and express information technology using standard unit vectors.
and express information technology using standard unit vectors.
![]()
![]()
![]()
![]() where
where ![]()
Decide whether ![]() and
and ![]() are equivalent vectors, where
are equivalent vectors, where ![]() and
and ![]()
Equivalent vectors
For the post-obit exercises, find vector ![]() with a magnitude that is given and satisfies the given conditions.
with a magnitude that is given and satisfies the given conditions.
a. ![]() b.
b. ![]()
A box is pulled ![]() yd horizontally in the ten-direction by a constant forcefulness
yd horizontally in the ten-direction by a constant forcefulness ![]() Find the deportation vector in component form.
Find the deportation vector in component form.
A 5-kg pendant chandelier is designed such that the alabaster bowl is held past four chains of equal length, as shown in the following effigy.
- Detect the magnitude of the force of gravity interim on the chandelier.
- Find the magnitudes of the forces of tension for each of the four bondage (assume chains are essentially vertical).

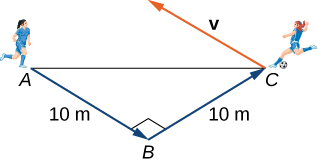
2 soccer players are practicing for an upcoming game. Ane of them runs 10 k from point A to point B. She so turns left at ![]() and runs 10 thousand until she reaches point C. And so she kicks the ball with a speed of x one thousand/sec at an upward bending of
and runs 10 thousand until she reaches point C. And so she kicks the ball with a speed of x one thousand/sec at an upward bending of ![]() to her teammate, who is located at betoken A. Write the velocity of the ball in component form.
to her teammate, who is located at betoken A. Write the velocity of the ball in component form.
a. ![]() (each component is expressed in centimeters per 2nd);
(each component is expressed in centimeters per 2nd); ![]() (expressed in centimeters per 2nd);
(expressed in centimeters per 2nd); ![]() (each component expressed in centimeters per second squared);
(each component expressed in centimeters per second squared);
b.
Source: https://opentextbc.ca/calculusv3openstax/chapter/vectors-in-three-dimensions/
0 Response to "What Is the Equation of the Line Tangent to the Curve Xy + 1 + E = Eã¢ë†â€™xy at the Point (1, âë†â€™1)?"
Post a Comment